- Nov 06, 2017 C Program To Calculate x^y Without Using pow Function - Duration: 5:39. C Plus+ 4,855 views.
- Sep 13, 2011 This site uses cookies. By continuing to use this site, you are agreeing to our use of cookies.
- Dev C Exponential Function Definition
- Dev C Exponential Function Formula
- Dev C Exponential Function Calculator
Mar 02, 2017 Program for Exponential Series in C is used to calculate the value of exp(x) for n number of terms using for loop and prints it in the output screen. Contact Us Privacy. Mar 02, 2017 Before going to the program for Exponential Series first let us understand what is a Exponential Series? Exponential Series: Exponential Series is a series which is used to find the value of e x. The formula used to express the e x as Exponential Series is. Expanding the above notation, the formula of Exponential Series is. The exp function computes, the base-e exponential of x. The exp2 function computes, the base-2 exponential of x. The expm1 function computes the base-e exponential of x, minus 1, accurately even for very small values of x.
| Language | ||||
| Standard Library Headers | ||||
| Freestanding and hosted implementations | ||||
| Named requirements | ||||
| Language support library | ||||
| Concepts library(C++20) | ||||
| Diagnostics library | ||||
| Utilities library | ||||
| Strings library | ||||
| Containers library | ||||
| Iterators library | ||||
| Ranges library(C++20) | ||||
| Algorithms library | ||||
| Numerics library | ||||
| Input/output library | ||||
| Localizations library | ||||
| Regular expressions library(C++11) | ||||
| Atomic operations library(C++11) | ||||
| Thread support library(C++11) | ||||
| Filesystem library(C++17) | ||||
| Technical Specifications |
| Common mathematical functions | ||||
| Mathematical special functions(C++17) | ||||
| Mathematical constants(C++20) | ||||
| Floating-point environment(C++11) | ||||
| Complex numbers | ||||
| Numeric arrays | ||||
| Pseudo-random number generation | ||||
| Compile-time rational arithmetic(C++11) | ||||
| Numeric algorithms | ||||
(C++17) | ||||
(C++17) | ||||
| Interpolations | ||||
(C++20) | ||||
(C++20) | ||||
| Generic numeric operations | ||||
(C++11) | ||||
(C++17) | ||||
(C++17) | ||||
(C++17) | ||||
(C++17) | ||||
(C++17) | ||||
(C++17) | ||||
| Bit operations | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) | ||||
(C++20) |
| Member functions | ||||||||||||||||
| Non-member functions | ||||||||||||||||
|
| |||||||||||||||
| Exponential functions | ||||||||||||||||
| Power functions | ||||||||||||||||
| Trigonometric functions | ||||||||||||||||
| ||||||||||||||||
| Hyperbolic functions | ||||||||||||||||
| ||||||||||||||||
template<class T > complex<T> exp(const complex<T>& z ); |
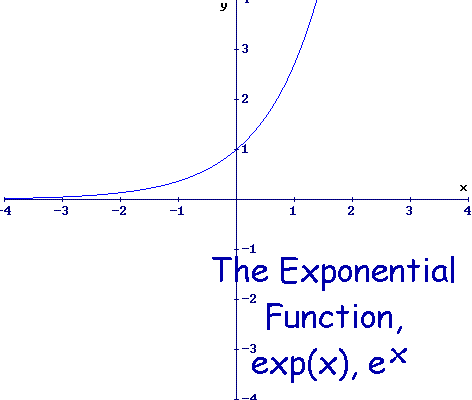
Compute base-e exponential of z, that is e (Euler's number, 2.7182818) raised to the z power.
[edit]Parameters
| z | - | complex value |
Dev C Exponential Function Definition
[edit]Return value
If no errors occur, e raised to the power of z, ez
, is returned.
[edit]Error handling and special values
Errors are reported consistent with math_errhandling
If the implementation supports IEEE floating-point arithmetic,
- std::exp(std::conj(z))std::conj(std::exp(z))
- If
zis(±0,+0), the result is(1,+0) - If
zis(x,+∞)(for any finite x), the result is(NaN,NaN)and FE_INVALID is raised. - If
zis(x,NaN)(for any finite x), the result is(NaN,NaN)and FE_INVALID may be raised. - If
zis(+∞,+0), the result is(+∞,+0) - If
zis(-∞,y)(for any finite y), the result is+0cis(y) - If
zis(+∞,y)(for any finite nonzero y), the result is+∞cis(y) - If
zis(-∞,+∞), the result is(±0,±0)(signs are unspecified) - If
zis(+∞,+∞), the result is(±∞,NaN)and FE_INVALID is raised (the sign of the real part is unspecified) - If
zis(-∞,NaN), the result is(±0,±0)(signs are unspecified) - If
zis(+∞,NaN), the result is(±∞,NaN)(the sign of the real part is unspecified) - If
zis(NaN,+0), the result is(NaN,+0) - If
zis(NaN,y)(for any nonzero y), the result is(NaN,NaN)and FE_INVALID may be raised - If
zis(NaN,NaN), the result is(NaN,NaN)
where cis(y) is cos(y) + i sin(y)

[edit]Notes
The complex exponential function ez
for z = x+iy equals ex
cis(y), or, ex
(cos(y) + i sin(y))
The exponential function is an entire function in the complex plane and has no branch cuts.
[edit]Example
Output:
[edit]See also
Dev C Exponential Function Formula
| complex natural logarithm with the branch cuts along the negative real axis (function template)[edit] | |
(C++11)(C++11) | returns e raised to the given power (ex) (function)[edit] |
| applies the function std::exp to each element of valarray (function template)[edit] | |
C documentation for cexp | |



